Menger Sponge

Created 2/12/2024

I have always been fascinated with the possibilities of modular origami. This subset of the hobby combines the "softness" of origami with rigid mathematical implications. The modular units I use are called the "Sonobe Module".

To construct a sonobe unit, watch this video.

As we will get to, large projects require hundreds of these units. Most of the time spent will be used folding and creating the units.

Sonobe units have slots in them that allow for the ends of other units to be inserted. This is how the modular design starts. From here, depending on how you put together and fold the underlying unit, many shapes can arise. However, I will be focusing on the menger sponge.

The menger sponge is a fractal that is constructed from a solid cube, and then popping holes into the center. And then, you subdivide each side of the cube into 8 sections, and then pop holes in the middle of the new sections, and then repeat.

Since each iteration can always be subdivided into squares, the menger sponge can always at each level be constructed with sonobe units. This is because the unit ends up as a square at the end.

Level 0 of the fractal (or just a cube), requires only 6 units. The initial size of the origami paper determines the size of the resulting cube.

Level 0 of the fractal (or just a cube), requires only 6 units. If you fold and unfold a unit, you will be able to see a diamond. From there, you can easily calculate the side length using the Pythagorean Theorem.

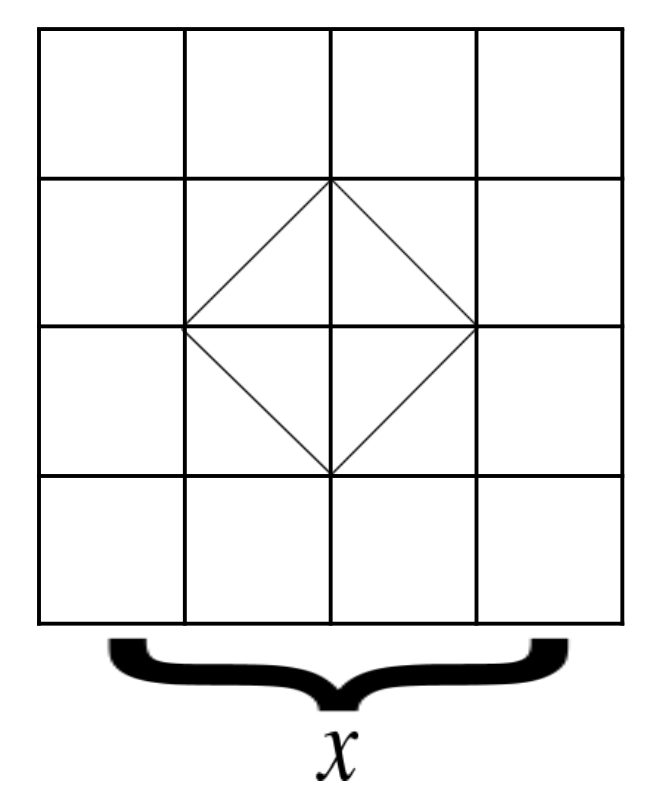
If we have the initial side length x and the unit side length l, then:

\[\begin{split} \left(\frac{x}{4}\right)^2 + \left(\frac{x}{4}\right)^2 &= l^2 \\ 2\left(\frac{x}{4}\right)^2 &= l^2 \\ \frac{x^2}{8} &= l^2 \\ \frac{x}{\sqrt{8}} = \frac{\sqrt{2}x}{4} &= l \end{split}\]

And so the resulting cube length will be $\frac{\sqrt{2}}{4}$ of the original square length. I would say that working with 3" by 3" paper works the best, as it results in a cube length of about 1 inch (1.06"). If you don't have access to this size of origami paper, you can use Sticky Notes, as they are commonly this size. If you have access to 1' by 1' paper, you can cut sheets in 16ths and have adequate size.

Level 0 of the menger sponge can be made in 5 minutes or so. However, moving to level 1 requires a bit more effort. Level 0 requires 6 units (as there are 6 sides of a cube), but how many units are required for this level? If you are familiar with the Rubik's cube, I will be using similar terminology to describe. You can think of going up a level as continually popping smaller and smaller holes into the cube, or you can think of it as creating 20 copies of the original, and glueing them together. (A Rubik's cube as 12 corners and 8 edges; 20 pieces). However, by glueing 20 copies together, there will be places where edges aren't needed.

If you look at the fractal image above, you can see there are sides of the structure that if we were glueing together complete tiny cubes, certain sides would not need to be there.

So, you can imagine starting a level 1 menger sponge by glueing together 20 cubes. These 20 cubes can be divided into 8 corners and 12 edges. Corners connect to edges in 3 different places, and edges connect to corners in 2. That means, for the 6 sides of a corner (there are 6 sides in a cube), 3 sides are not needed, and for the 6 sides of a edge, 2 sides are not needed. This is because a corner has 3 sides of itself hidden, meaning we don't need to make the units for those places. Similarly, an edge has 2 sides of itself hidden. So we can calculate the number like so:

\[\begin{split} n_{\text{max}} &= 20 \cdot 6 \\ n_{\text{max}} &= 8 \cdot 6 + 12 \cdot 6 \\ n &= 8 \cdot (6 - 3) + 12 \cdot (6 - 2) \\ n &= 24 + 48 \\ n &= 72 \end{split}\]

Thus, 72 units are needed to construct a level 1 Menger Sponge.

Here are a couple things I would recommend:

Don't fold the ends until all 72 are folded. How the edges will be folded is determined by what kind of piece you will need when constructing.
Start with a corner, build the bottom, and then collectively work your way up.
The "face" side of all the units should be the only side visible. Using this, you can hold a piece in a position, and know how the edges should be folded to fit into local units.

What about level 2? When I first accomplished level 1, it actually took me 3 months to make. It can me made in 2-4 hours, however, I was just really lazy. I thought that if level 1 took me that long, how long would level 2 take? I didn't dare try until a year and half later in 2022 I attempted the challenge.

The units needed for level 2 jump up exponentially. $n_{max}$ is now 72*20 = 1440. Going at the same pace as my level 1 build, it would take me 5 years just to fold 1440 units (24 units/month). However, 1440 is just the max. What is the actual number needed?

If we follow the same process as before, we can arrive at the result. We can break $n_{max}$ into 8 corners (8 * 72) and 12 edges (12 * 72). Not all of the 72 units for the corners and edges are needed. 3 sides of each corner are hidden. Note that since each corner is level 1, each side contains 8 squares. That means we can subtract 8 * 3 from the 72 for each corner. Similar, we can subtract 8 * 2 from each edge. This results in:

\[\begin{split} n_{\text{max}} &= 20 \cdot 72 \\ n_{\text{max}} &= 8 \cdot 72 + 12 \cdot 72 \\ n &= 8 \cdot (72 - 3 \cdot 8) + 12 \cdot (72 - 2 \cdot 8) \\ n &= 384 + 672 \\ n &= 1056 \end{split}\]

With these two examples, we can generalize this to a sequence, $a_{n}$ . $n_{max}$ will always be $20 a_{n - 1}$ , where n is the level. We can break this apart into $8 a_{n - 1} + 12 a_{n - 1}$ . From there, the number of units needed for each corner and cube will need to be reduced. Each corner will need to by subtracted some multiple of $8^{n}$ . We know this is the case as when we were first discussing how to make a menger sponge, each level's side is subdivided in 8. As such, since 3 sides of a corner is hidden, the amount of units we won't use are $3 * 8^{n}$ , and the amount of units we won't use for edges are $2 * 8^{n}$ , since 2 sides of each edge are hidden. And so:

\[\begin{split} a_n &= 8 \cdot ( a_{n-1} - 3 \cdot 8^{n-1} ) + 12 \cdot ( a_{n-1} - 2 \cdot 8^{n-1} ) \\ a_n &= 8a_{n-1} - 24 \cdot \frac{8^n}{8} + 12a_{n-1} - 24 \cdot \frac{8^n}{8} \\ a_n &= 20a_{n-1} - 6 \cdot 8^n\\ \end{split}\]

We now have a recursive formula for knowing how many units are required per level. It is important to consider why this formula makes sense. If you consider a Rubik's cube, there 6 planes of rotation.

And if I were to take one of these slices out:

You can see that the inside of each slice also has 8 "squares", just like the outside. This applies to each level of the menger sponge. The are 6 slices where edge and corner interact, and for example if you were to slice a level 2 at one of these planes, it would look like this:

Which consists of $8^{n}$ squares, and as such the original equation of $a_{n} = 20 a_{n - 1} - 6 * 8^{n}$ makes sense. And yes, I did build a level 2 menger sponge. I took me around 8 months of work. Here is the timeline:

The first picture was dated March 26, 2021, and the last picture was dated November 23, 2021. This project could have definitely been done in a month, but it would have required 3-4 hours each day. Most of the time spent was folding and creating the units. I started folded on March 26, and got done October 21. 86% of the time was spend folding (209 days / 242 days).

The only thing that doesn't sit right for me is that our current equation is recursive. Any good mathematician would try and produce an explicit formula. It can be done, but it requires a bit of algebra. The only thing of note in the algebra is the use of the geometric series formula, and that additive inverses were made to complete the series.

\[\begin{split} a_n &= 20a_{n-1} - 6 \cdot 8^n \\ &= 20(20a_{n-2} - 6 \cdot 8^{n-1}) - 6 \cdot 8^n \\ &= 20^2a_{n-2} - 20 \cdot 6 \cdot 8^{n-1} - 6 \cdot 8^n \\ &= 20^2(a^{n-3}-6\cdot8^{n-2})-20\cdot6\cdot6^{n-1}-6\cdot8^n\\ &\;\;\vdots \\ &= 20^{n-1}a_{n-(n-1)}-20^{n-2}\cdot6\cdot8^2-20^{n-3}\cdot6\cdot8^3-\dots-6\cdot8^n \\ &= 20^{n-1}a_{1}-20^{n-2}\cdot6\cdot8^2-20^{n-3}\cdot6\cdot8^3-\dots-6\cdot8^n \\ &= \frac{20^n}{20}a_1-\frac{20^n}{20^2}\cdot6\cdot8^2-\frac{20^n}{20^3}\cdot6\cdot8^3-\dots-\frac{20^n}{20^n}6\cdot8^n \\ &= 6\cdot20^n\left(\frac{12}{20}-\frac{8^2}{20^2}-\frac{8^3}{20^3}-\dots-\frac{8^n} {20^n}\right) \\ &= 6\cdot20^n\left(\frac{12}{20}+\frac{2}{5}+1-\left(\frac{2}{5}\right)^0-\left(\frac{2}{5}\right)^1-\left(\frac{2}{5}\right)^2-\dots-\left(\frac{2}{5}\right)^n\right) \\ &= 6\cdot20^n\left(2-\left(\frac{1-(2/5)^{n+1}}{1-2/5}\right)\right) \\ &= 6\cdot20^n\left(2-\left((1-(2/5)^n(2/5))\cdot\frac{20}{12}\right)\right) \\ &= 6\cdot20^n\left(2-\left(\frac{5}{3}-\frac{2}{3}\left(\frac{2} {5}\right)^n\right)\right) \\ &= 20^n\left(2+4\left(\frac{2}{5}\right)^n\right) \\ &= 2\cdot20^n + 4\cdot8^n \end{split}\]

WolframAlpha keeps telling me that the formula can be even more simplified, but I don't believe it. Simplify the equation in WolframAlpha and you'll see this is the simplest it can get.